向量叉积

在数学和向量代数领域，向量叉积（英语：Cross product）又称向量积（英语：Vector product），是对三维空间中的两个向量的二元运算，使用符号$$\times$$。与点积不同，它的运算结果是向量。对于线性无关的两个向量 $$\mathbf {a}$$ 和$$\mathbf {b}$$ ，它们的叉积写作 $${\displaystyle \mathbf {a} \times \mathbf {b} }$$，是 $$\mathbf {a}$$ 和 $$\mathbf {b}$$ 所在平面的法线向量，与$$\mathbf {a}$$ 和$$\mathbf {b}$$ 都垂直。叉积被广泛运用于数学、物理、工程学、计算机科学领域。

如果两个向量方向相同或相反（即它们非线性无关），亦或任意一个的长度为零，那么它们的叉积为零。推广开来，叉积的模长和以这两个向量为边的平行四边形的面积相等；如果两个向量成直角，它们叉积的模长即为两者长度的乘积。

叉积和点积一样依赖于欧几里德空间的度量，但与点积之不同的是，叉积还依赖于定向或右手定则。

向量叉积的定义

使用右手定则确定叉积的方向
两个向量 $$\mathbf {a}$$ 和 $$\mathbf {b}$$ 的叉积仅在三维空间中有定义，写作 $${\displaystyle \mathbf {a} \times \mathbf {b} }$$。在物理学中，叉积有时也被写成$${\displaystyle \mathbf {a} \wedge \mathbf {b} }$$，但在数学中 $${\displaystyle \mathbf {a} \wedge \mathbf {b} }$$ 是外代数中的外积。

叉积 $${\displaystyle \mathbf {a} \times \mathbf {b} }$$ 是与 $$\mathbf {a}$$ 和 $$\mathbf {b}$$ 都垂直的向量$$\mathbf {c}$$ 。其方向由右手定则决定，模长等于以两个向量为边的平行四边形的面积。

叉积可以定义为：

$${\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\ \mathbf {n} }$$
其中 $$\theta$$ 表示 $$\mathbf {a}$$ 和 $$\mathbf {b}$$ 在它们所定义的平面上的夹角$$（{\displaystyle 0^{\circ }\leq \theta \leq 180^{\circ }}）$$。$${\displaystyle |\mathbf {a} |}$$和 $${\displaystyle |\mathbf {b} |}$$ 是向量$$\mathbf {a}$$ 和 $$\mathbf {b}$$ 的模长，而 $$\mathbf{n}$$ 则是一个与 $$\mathbf {a}$$ 、$$\mathbf {b}$$ 所构成的平面垂直的单位向量，方向由右手定则决定。根据上述公式，当 $$\mathbf {a}$$ 与 $$\mathbf {b}$$ 平行（即 $$\theta$$ 为 0° 或 180°）时，它们的叉积为零向量 $$\mathbf{0}$$。

叉积a × b（垂直方向、紫色）随着向量 a（蓝色）和 b（红色）的夹角变化。 叉积垂直于两个向量，模长在两者平行时为零、在两者垂直时达到最大值‖a‖‖b‖。
按照惯例，向量 $$\mathbf{n}$$ 的方向由右手定则决定：将右手食指指向 $$\mathbf {a}$$ 的方向、中指指向 $$\mathbf {b}$$ 的方向，则此时拇指的方向即为 $$\mathbf{n}$$ 的方向。使用这一定则意味着叉积满足反交换律，$${\displaystyle \mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} )}$$：将右手食指指向$$\mathbf {b}$$ 、中指指向 $$\mathbf {a}$$ ，那么拇指就必定指向相反方向，即翻转了叉积的符号。

由此可以看出，使用叉积需要考虑坐标系的利手性（英语：Handedness），如果使用的是左手坐标系，向量$$\mathbf{n}$$ 的方向需要使用左手定则决定，与右手坐标系中的方向相反。

这样就会带来一个问题：参照系的变换不应该影响 $$\mathbf{n}$$ 的方向（例如从右手坐标系到左手坐标系的镜像变换）。因此，两个向量的叉积并不是（真）向量，而是伪向量。

向量叉积的计算

向量叉积的坐标表示

基向量$$（i、j、k，也记作 e1、e2、e3）$$和向量 a 的分解$$（ax、ay、az，也记作 a1、a2、a3)$$
右手坐标系中，基向量$${\mathbf {i}}$$、$$\mathbf{j}$$、$$\mathbf{k}$$ 满足以下等式：

$${\displaystyle {\begin{aligned}\mathbf {i} \times \mathbf {j} &=\mathbf {k} \\ \mathbf {j} \times \mathbf {k} &=\mathbf {i} \\ \mathbf {k} \times \mathbf {i} &=\mathbf {j} \end{aligned}}}$$
根据反交换律可以得出：

$${\displaystyle {\begin{aligned}\mathbf {j\times i} &=-\mathbf {k} \\ \mathbf {k\times j} &=-\mathbf {i} \\ \mathbf {i\times k} &=-\mathbf {j} \end{aligned}}}$$
根据叉积的定义可以得出：
$${\displaystyle \mathbf {i} \times \mathbf {i} =\mathbf {j} \times \mathbf {j} =\mathbf {k} \times \mathbf {k} =\mathbf {0} }$$（零向量）。
根据以上等式，结合叉积的分配律和线性关系，就可以确定任意向量的叉积。

向量 $$\mathbf{u}$$ 和 $$\mathbf {v}$$ 可以定义为平行于基向量的三个正交元素之和：

$${\displaystyle {\begin{aligned}\mathbf {u} &=u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} \\ \mathbf {v} &=v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} \end{aligned}}}$$
两者的叉积 $${\displaystyle \mathbf {u} \times \mathbf {v} }$$ 可以根据分配律展开：

$${\displaystyle {\begin{aligned} \mathbf {u} \times \mathbf {v} =(u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} )\times (v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} )\\ =u_{1}v_{1}(\mathbf {i} \times \mathbf {i} )+u_{1}v_{2}(\mathbf {i} \times \mathbf {j} )+u_{1}v_{3}(\mathbf {i} \times \mathbf {k} )+\\ u_{2}v_{1}(\mathbf {j} \times \mathbf {i} )+u_{2}v_{2}(\mathbf {j} \times \mathbf {j} )+u_{2}v_{3}(\mathbf {j} \times \mathbf {k} )+\\ u_{3}v_{1}(\mathbf {k} \times \mathbf {i} )+u_{3}v_{2}(\mathbf {k} \times \mathbf {j} )+u_{3}v_{3}(\mathbf {k} \times \mathbf {k} ) \end{aligned}}}$$
即把 $${\displaystyle \mathbf {u} \times \mathbf {v} }$$ 分解为九个仅涉及 $${\mathbf {i}}$$、$$\mathbf{j}$$、$$\mathbf{k}$$ 的简单叉积之和。九个叉积各自所涉及的向量，要么相互平行、要么相互正交。将最前面所述的几个等式带入其中，然后合并同类项，可以得到：
$${\displaystyle {\begin{aligned} \mathbf {u} \times \mathbf {v} =\\ -u_{1}v_{1}\mathbf {0} +u_{1}v_{2}\mathbf {k} -u_{1}v_{3}\mathbf {j} \\ -u_{2}v_{1}\mathbf {k} -u_{2}v_{2}\mathbf {0} +u_{2}v_{3}\mathbf {i} \\ +u_{3}v_{1}\mathbf {j} -u_{3}v_{2}\mathbf {i} -u_{3}v_{3}\mathbf {0} \\ =(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}}$$
即结果向量 $${\displaystyle \mathbf {s} =s_{1}\mathbf {i} +s_{2}\mathbf {j} +s_{3}\mathbf {k} =\mathbf {u} \times \mathbf {v} }$$的三个标量元素为：

$${\displaystyle {\begin{aligned}s_{1}&=u_{2}v_{3}-u_{3}v_{2}\\ s_{2}&=u_{3}v_{1}-u_{1}v_{3}\\ s_{3}&=u_{1}v_{2}-u_{2}v_{1}\end{aligned}}}$$
也可以记作列向量的形式：
$${\displaystyle {\begin{pmatrix}s_{1}\\s_{2}\\s_{3}\end{pmatrix}}={\begin{pmatrix}u_{2}v_{3}-u_{3}v_{2}\\u_{3}v_{1}-u_{1}v_{3}\\u_{1}v_{2}-u_{2}v_{1}\end{pmatrix}}}$$

向量叉积的矩阵表示

根据萨吕法则确定 u 和 v 的叉积
叉积可以表达为这样的行列式：

$${\displaystyle \mathbf {u\times v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\ u_{1}&u_{2}&u_{3}\\ v_{1}&v_{2}&v_{3} \end{vmatrix}}}$$
这个行列式可以使用萨吕法则或拉普拉斯展开计算。使用萨吕法则可以展开为：
$${\displaystyle {\begin{aligned}\mathbf {u\times v} =\\ (u_{2}v_{3}\mathbf {i} +u_{3}v_{1}\mathbf {j} +u_{1}v_{2}\mathbf {k} )-(u_{3}v_{2}\mathbf {i} +u_{1}v_{3}\mathbf {j} +u_{2}v_{1}\mathbf {k} )=\\ (u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}}$$
使用拉普拉斯展开可以沿第一行展开为：
$${\displaystyle {\begin{aligned}\mathbf {u\times v} ={\begin{vmatrix}u_{2}&u_{3}\\v_{2}&v_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}u_{1}&u_{3}\\v_{1}&v_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}u_{1}&u_{2}\\v_{1}&v_{2}\end{vmatrix}}\mathbf {k} =\\ (u_{2}v_{3}-u_{3}v_{2})\mathbf {i} -(u_{1}v_{3}-u_{3}v_{1})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}}$$
都可以直接得到结果向量。

向量叉积的性质

向量叉积的代数性质

对于任意三个向量 $$\mathbf {a}$$ 、$$\mathbf {b}$$ 、$$\mathbf {c}$$ ，
$${\displaystyle \mathbf {a} \times \mathbf {a} =\mathbf {0} }$$
$${\displaystyle \mathbf {a} \times \mathbf {0} =\mathbf {0} }$$
$${\displaystyle \mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} )}$$（反交换律）
$${\displaystyle \mathbf {a} \times (\mathbf {b} +\mathbf {c} )=\mathbf {a} \times \mathbf {b} +\mathbf {a} \times \mathbf {c} }$$（加法的左分配律）
$${\displaystyle (\mathbf {a} +\mathbf {b} )\times \mathbf {c} =\mathbf {a} \times \mathbf {c} +\mathbf {b} \times \mathbf {c} }$$（加法的右分配律）
$${\displaystyle (\lambda \mathbf {a} )\times \mathbf {b} =\lambda (\mathbf {a} \times \mathbf {b} )=\mathbf {a} \times (\lambda \mathbf {b} )}$$
$${\displaystyle \mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} }$$
$${\displaystyle |\mathbf {a} \times \mathbf {b} |=|\mathbf {b} \times \mathbf {a} |}$$
$${\displaystyle |\mathbf {a} \times \mathbf {b} |^{2}=|\mathbf {a} |^{2}|\mathbf {b} |^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}={\begin{vmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\ \mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \end{vmatrix}}}$$（拉格朗日恒等式）
一般来说，向量叉积不遵守约简律，即 $${\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {a} \times \mathbf {c} }$$ 不表示 $${\displaystyle \mathbf {b} =\mathbf {c} }$$。此外，$${\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {0} }$$ 不表示 $${\displaystyle \mathbf {a} =\mathbf {0} }$$ 或 $${\displaystyle \mathbf {b} =\mathbf {0} }$$。

但对于两个非零向量 $$\mathbf {a}$$ 和 $$\mathbf {b}$$ ，

• $${\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {0} } $$当且仅当 $$\mathbf {a}$$ 平行于 $$\mathbf {b}$$

向量叉积的几何意义

如果以向量$$\mathbf {a}$$ 和 $$\mathbf {b}$$ 为边构成一个平行四边形，那么这两个向量叉积的模长与这个平行四边形的正面积相等（如图1）：

图1：平行四边形面积即叉积的模长

$${\displaystyle \left|\mathbf {a} \times \mathbf {b} \right|=\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin \theta .}$$
同时，如果以向量$$\mathbf {a}$$、$$\mathbf {b}$$ 、$$\mathbf {c}$$为棱构成一个平行六面体，那么这个平行六面体的体积$${\mathbf {V}}$$ 也可以通过叉积和点积的组合得到，这种积称作标量三重积（如图2）：

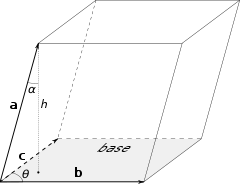
图2：三个向量定义平行六面体

$${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).}$$
因为标量三重积可能为负，平行六面体的体积需要取其绝对值：

$${\displaystyle V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}$$
因为叉积的模长与其参数夹角的正弦有关，可以认为叉积是“垂直度”的度量，正如点积是“平行度”的度量一样。对于任意两个单位向量，叉积为1意味着它们互相垂直，叉积为0意味着它们互相平行。点积则相反：点积为0意味着它们互相垂直。

单位向量还能带来两个特性：两个单位向量的点积是它们夹角的余弦（可正可负）；它们叉积的模长则为夹角的正弦（始终为正）。

向量微分

对于实数 {\displaystyle t}t 和两个向量值函数 $${\displaystyle \mathbf {a} (t)}$$、$${\displaystyle \mathbf {b} (t)}$$，乘积法则成立：

$${\displaystyle {\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}}}$$

三维坐标

给定直角坐标系的单位向量$$\mathbf {i}$$，$$\mathbf{j}$$，$$\mathbf{k}$$满足下列等式：

$${\displaystyle \mathbf {i} \times \mathbf {j} =\mathbf {k} }$$、
$${\displaystyle \mathbf {j} \times \mathbf {k} =\mathbf {i} }$$、
$${\displaystyle \mathbf {k} \times \mathbf {i} =\mathbf {j} }$$
通过这些规则，两个向量的叉积的坐标可以方便地计算出来，不需要考虑任何角度：设

$${\displaystyle \mathbf {a} =a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k} }$$
$${\displaystyle \mathbf {b} =b_{1}\mathbf {i} +b_{2}\mathbf {j} +b_{3}\mathbf {k} }$$
则
$${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} = (a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} =\\ {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3} \end{vmatrix}} \end{aligned}}}$$
叉积也可以用四元数来表示。注意到上述 $${\mathbf {i}}$$、$$\mathbf{j}$$、$$\mathbf{k}$$ 之间的叉积满足四元数的乘法。一般而言，若将向量$$[a_1, a_2, a_3]$$表示成四元数$$a_1i + a_2j + a_3k$$，两个向量的叉积可以这样计算：计算两个四元数的乘积得到一个四元数，并将这个四元数的实部去掉，即为结果。更多关于四元数乘法，向量运算及其几何意义请参见四元数与空间旋转。