向量运算

向量的大小是相对的，在有需要时，会规定单位向量，以其长度作为1。每个方向上都有一个单位向量。

向量之间可以如数字一样进行运算。本文介绍向量基本运算公式，常见的向量运算有：加法、减法、数与向量之间的乘法（数量积）以及向量与向量之间的乘法（向量积）。

加法与减法

向量的加法满足平行四边形法则和三角形法则。具体地，两个向量$$\vec{a}$$和$$\vec{b}$$相加，得到的是另一个向量。这个向量可以表示为$$\vec{a}$$和$$\vec{b}$$的起点重合后，以它们为邻边构成的平行四边形的一条对角线（以共同的起点为起点的那一条，见下图左），或者表示为将$$\vec{a}$$的终点和$$\vec{b}$$的起点重合后，从$$\vec{a}$$的起点指向$$\vec{b}$$的终点的向量：

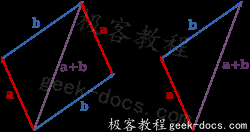
向量 a 加向量 b

两个向量$$\vec{a}$$和$$\vec{b}$$的相减，则可以看成是向量$$\vec{a}$$加上一个与$$\vec{b}$$大小相等，方向相反的向量。又或者，$$\vec{a}$$和$$$\vec{b}$$的相减得到的向量可以表示为$$\vec{a}$$和$$\vec{b}$$的起点重合后，从$$\vec{b}$$的终点指向$$\vec{a}$$的终点的向量：

向量 a 减向量 b

当这两个向量数值、方向都不同，基本向量$$\vec{e}_1=(1,0,0),\vec{e}_2=(0,1,0),\vec{e}_3=(0,0,1)$$时，向量和计算为

$$\vec{a}+\vec{b} =(a_1+b_1)\vec{e}_1 +(a_2+b_2)\vec{e}_2 +(a_3+b_3)\vec{e}_3$$
并且有如下的不等关系：

$$\left |\vec{a} \right | +\left |\vec{b} \right | \ge \left |\vec{a}+\vec{b} \right | \ge \left |\vec{a} \right | – \left |\vec{b} \right |$$
此外，向量的加法也满足交换律和结合律。

向量与积

向量空间分为有限维向量空间与无限维向量空间。在有限维向量空间中，可以找到一组（有限个）向量$$\vec{e}_1, \vec{e}_2, \cdots , \vec{e}_n$$，使得任意一个向量$$\vec{v}$$都可以唯一地表示成这组向量的线性组合：

$$\vec{v} =v_1 \vec{e}_1 + v_2 \vec{e}_2 + \cdots + v_n \vec{e}_n$$
其中的标量$$v_1, v_2, \cdots , v_n$$是随着向量$$\vec{v}$$而确定的。这样的一组向量称为向量空间的基。给定了向量空间以及一组基后，每个向量就可以用一个数组来表示了。两个向量$$\vec{v}$$和$$\vec{w}$$相同，当且仅当表示它们的数组一样。

$$\begin{array}{lcl} v_1 &=& w_1 \\ v_2 &=& w_2 \\ \vdots \ && \vdots \\ v_n &=& w_n \end{array}$$
两个向量$$\vec{v}$$和 $$\vec{w}$$的和：

$$\vec{v} + \vec{w} =(v_1 + w_1)\vec{e}_1 +(v_2 + w_2 ) \vec{e}_2 + \cdots +(v_n + w_n ) \vec{e}_n$$
它们的数量积为：

$$\vec{v} \cdot \vec{w} = v_1 \cdot w_1 + v_2 \cdot w_2 + \cdots + v_n \cdot w_n$$
而标量k与向量v的乘积则为：

$$k \cdot \vec{v} =(k \cdot v_1)\vec{e}_1 +(k \cdot v_2) \vec{e}_2 + \cdots +(k \cdot v_n) \vec{e}_n$$

标量乘法

一个标量k和一个向量$$\vec{v}$$之间可以做乘法，得出的结果是另一个与$$\vec{v}$$方向相同或相反，大小为$$\vec{v}$$的大小的｜k｜倍的向量，可以记成$$k\vec{v}$$。该种运算被称为标量乘法或数乘。-1乘以任意向量会得到它的反向量，0乘以任何向量都会得到零向量 $$\vec{0}$$。

数量积

数量积也叫点积，它是向量与向量的乘积，其结果为一个标量（非向量）。几何上，数量积可以定义如下：

设 $$\vec{a}$$、$$\vec{b}$$ 为两个任意向量，它们的夹角为$$\theta$$ ，则他们的数量积为：

$${\displaystyle {\vec {a}}\cdot {\vec {b}}=\left|{\vec {a}}\right|\left|{\vec {b}}\right|\cos {\theta }}$$
即 $$\vec{b}$$ 向量在 $$\vec{a}$$ 向量方向上的投影长度（同方向为正反方向为负号），与 $$\vec{a}$$ 向量长度的乘积。

向量积

向量积也叫叉积(向量叉乘)，外积，它也是向量与向量的乘积，不过需要注意的是，它的结果是个向量。它的几何意义是所得的向量与被乘向量所在平面垂直，方向由右手定则规定，大小是两个被乘向量张成的平行四边形的面积。所以向量积不满足交换律。举例来说 $$(1,0,0)\times (0,1,0)=(0,0,1)$$ 但是 $$(0,1,0)\times (1,0,0)=(0,0,-1)$$。

设有向量$${\displaystyle {\vec {a}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}+a_{z}{\vec {k}}}$$、$${\displaystyle {\vec {b}}=b_{x}{\vec {i}}+b_{y}{\vec {j}}+b_{z}{\vec {k}}}$$，

则其向量积的矩阵表达式可用下列符号表示：

$${\displaystyle {\vec {a}}\times {\vec {b}}}=$$
$${\begin{vmatrix} {\vec {i}}&{\vec {j}}&{\vec{k}} \\ a_{x}&a_{y}&a_{z} \\ b_{x}&b_{y}&b_{z} \end{vmatrix}}$$

混合积

三个向量$$\vec{a}、\vec{b}$$和$$\vec{c}$$的混合积定义为，物理意义为三向量始于同点时所构成的体积：

$$\vec{a}\cdot(\vec{b}\times \vec{c})= \vec{b}\cdot(\vec{c}\times \vec{a})= \vec{c}\cdot(\vec{a}\times \vec{b})$$

关于向量运算的定理

向量与定比分点、中点公式
在实际应用中，向量运算时常会运用到定比分点定理。

设平面直角坐标系$$Oxy$$原点$$O(0,0)$$，内有点$$A(x_1,y_1)$$，点$$B(x_2,y_2)$$，点$$P(x_0,y_0)$$，点$$P$$在点$$A、B$$之间，且

$$\left|\overrightarrow{A P}\right|:\left|\overrightarrow{P B}\right|=n$$，则：
$$\overrightarrow{O P}\left(\frac{x_1+nx_2}{1+n},\frac{y_1+ny_2}{1+n}\right)$$

特殊地，当$$n=1$$，
$$\overrightarrow{O P}=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$$
相应的有中点$$P$$坐标： $$\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$$
实际上，上述结论可以推广到空间向量中。
设空间直角坐标系$$Oxyz$$内原点为$$O(0,0,0)$$，有点$$A(x_1,y_1,z_1)$$，$$B(x_2,y_2,z_2)$$，$$A、B$$点间有一点$$P$$，且

$$\left|\overrightarrow{A P}\right|:\left|\overrightarrow{P B}\right|=n$$，
则：$$\overrightarrow{O P}=\left(\frac{x_1+nx_2}{1+n},\frac{y_1+ny_2}{1+n},\frac{z_1+nz_2}{1+n}\right)$$
中点$$P$$坐标：
$$\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2}\right)$$